Rebalancing a Portfolio
Introduction
Consider a simple portfolio of 4 stocks: AAPL, ALGN, AMZN, and EBAY. The daily price data for these stocks is downloaded from Yahoo Finance, for a 20-year period, from 2004 to 2023. Let \(P_{i,t}\) denote the price of stock \(i\) on day \(t\) with \(i = 1,2,3,4\).
For an investor focusing on this portfolio, suppose that the primary investment goal is to minimize overall volatility. Using the daily price data from 2004 to 2019, the MinimumVolatility portfolio estimator within the skportfolio library is employed to train the portfolio.
The resulting allocations for the optimised portfolio are as follows:
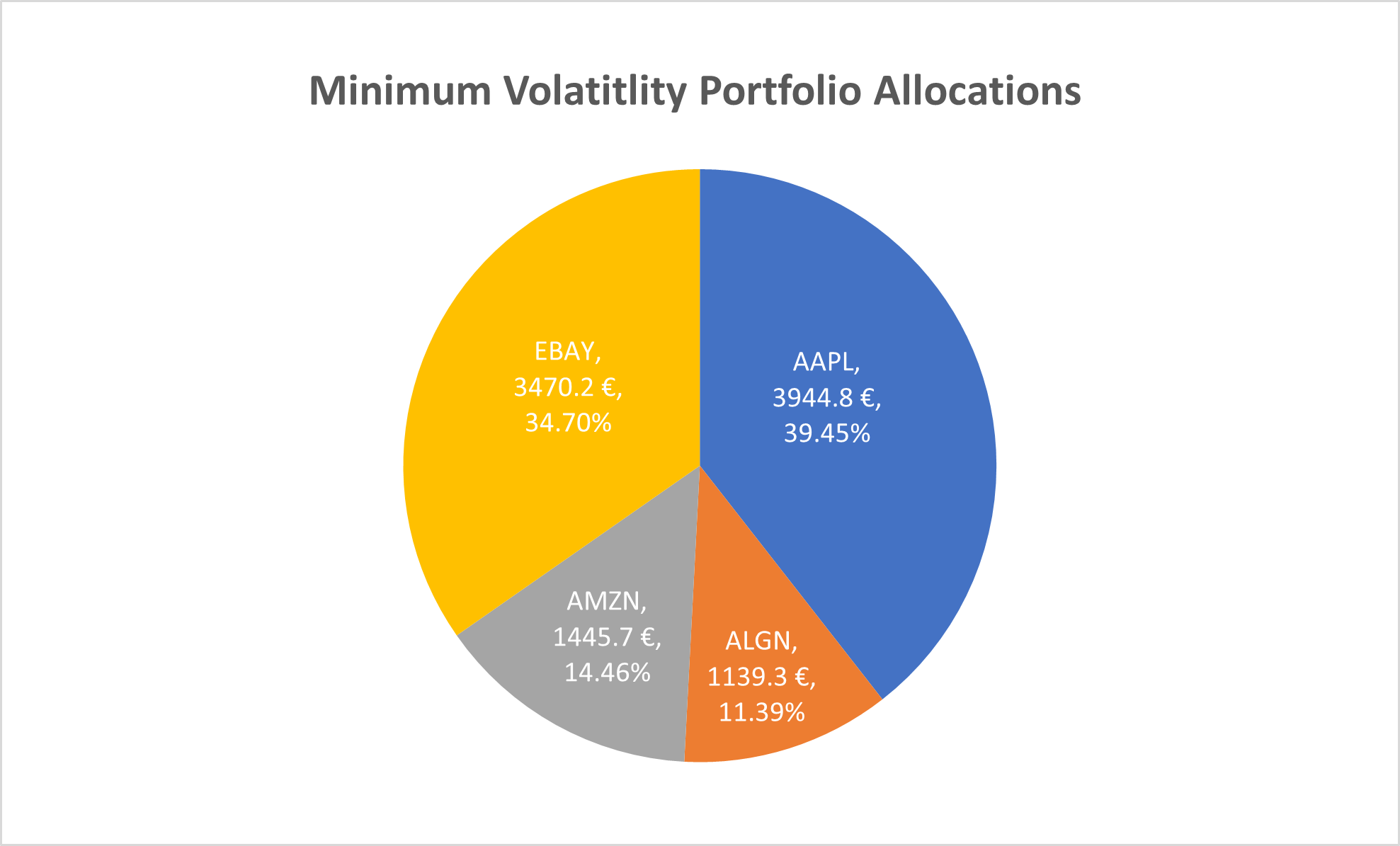
To assess the effectiveness of this allocation strategy, the portfolio is tested on the data from the year 2020. This is called a backtest as the true historical data is used to test our strategy.
Suppose that an initial amount of 10000 EUR is invested in this portfolio. The positions of the portfolio are the amount investment in each asset. Let \(Y_{i,t}\) denote the position of stock \(i\) on day \(t\) and \(W_{i,t}\) be the weight allocated to stock \(i\) on day \(t\). The portfolio returns or equity \(E_{t}\) on day \(t\) is the sum of all positions on day \(t\).
On Day 1 (January 2, 2020) of testing our allocation strategy, the initial portfolio positions are calculated as
\[Y_{i,1} = W_{i,1} \times E_{1}\] \[E_{1} = 10000\]where \(W_{i,0}\) are the initial weights predicted by our strategy.
For example, considering AAPL, \(W_{1,1} \approx 0.39\) and \(Y_{1,1} = W_{1,1} \times E_{1} = 3944\)
By the end of Day 2, the new close price data for the stocks are available. The daily returns \(R_{i,t}\) for each stock is calculated using
\[R_{i,t} = \frac{P_{i,t} - P_{i, t-1}}{ P_{i, t-1}}\]The current position, the amount invested in each asset changes in value according to the returns of the asset on that day. For example, the price of AAPL on Day 1 is \(P_{1,1} = 73.15\) and \(P_{1,2} = 72.44\) on Day 2. So the current position of the 3944 EUR in AAPL becomes,
\[R_{1,2} = -0.0097\] \[Y_{1,2} = (1+R_{1,2})\times Y_{1,1} = 3905.7\]This process repeats daily, causing fluctuations in the overall portfolio value. Over time, due to varying returns in different stocks, the weights of these assets within the portfolio naturally change. The figure below visualizes how these weights changed over a month.
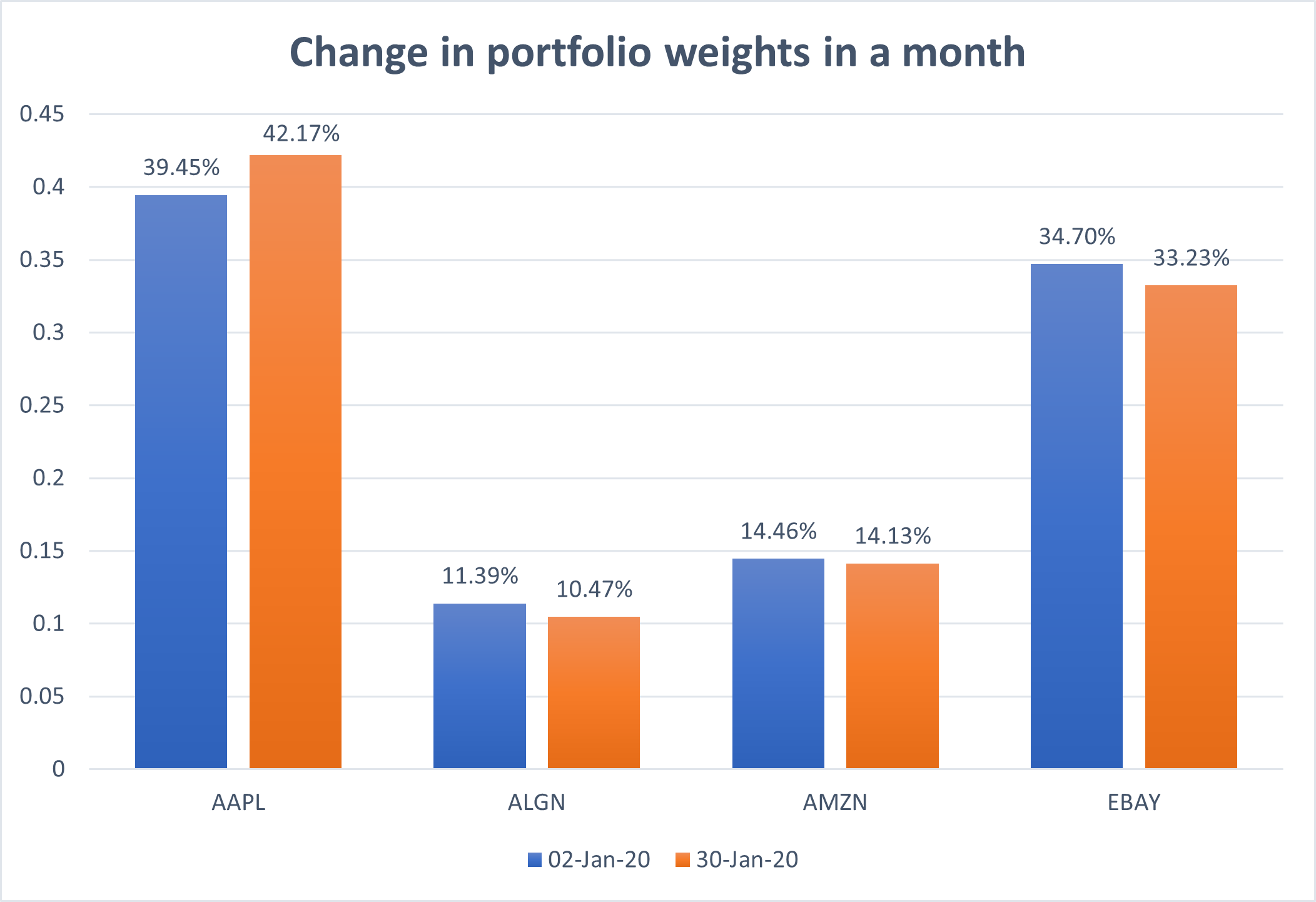
What could be the implications of this to the investor? The evolving nature of the portfolio’s composition implies that it may no longer align with the characteristics of the initially constructed Minimum Volatility portfolio and this directly influences the risk profile of the investment.
Rebalancing a portfolio is the process of changing the weights of assets in a portfolio back to its original target allocation. Periodic rebalancing is necessary to maintain the desired risk level and prevent any single asset from dominating performance.
To rebalance a portfolio, one has to buy or sell assets to reach their desired portfolio. In the example above, one has to sell AAPL and buy ALGN. However, it’s important to note that there are transaction costs associated with buying and selling assets. These costs can include brokerage fees, bid-ask spreads, and other expenses related to executing trades in the market.
Rebalancing Procedure
Suppose that the portfolio is rebalanced every 10 days.
On the first rebalancing day (Day 10 - January 15, 2020), the current proportion of weights is calculated as
\[W_{i, 10} = \frac{Y_{i,10}}{E_{10}}\]The change in asset allocation weights on this day is
\[\Delta W_{i,10} = W_{i, 10} - W_{i, 1}\]Assuming a standardized transaction cost of 1% for all assets, the transaction costs for each asset are determined by:
\[C_{i,10} = |\Delta W_{i, 10}| \times 0.01 \times Y_{i, 10}\] \[C_{10} = \sum_{i} C_{i,10}\]These transaction costs are deducted from the portfolio returns on the rebalancing day to obtain the adjusted portfolio returns:
\[E^*_{10} = E_{10} - C_{10}\]The updated portfolio returns on the rebalancing day are then reallocated using our initial strategy weights, and the new positions on Day 11 (January 15, 2020) are
\[Y_{i,11} = W_{i,1} \times E^*_{10}\]These steps are reiterated on the subsequent rebalancing day (Day 20 - 30 January, 2020)
\[E^*_{20} = E_{20} - (\sum_{i} |\Delta W_{i, 20}| * 0.01 * Y_{i, 20})\]The graph below with the equity curve with and without rebalancing provides a clear illustration of the impact of the rebalancing strategy on portfolio performance over time.
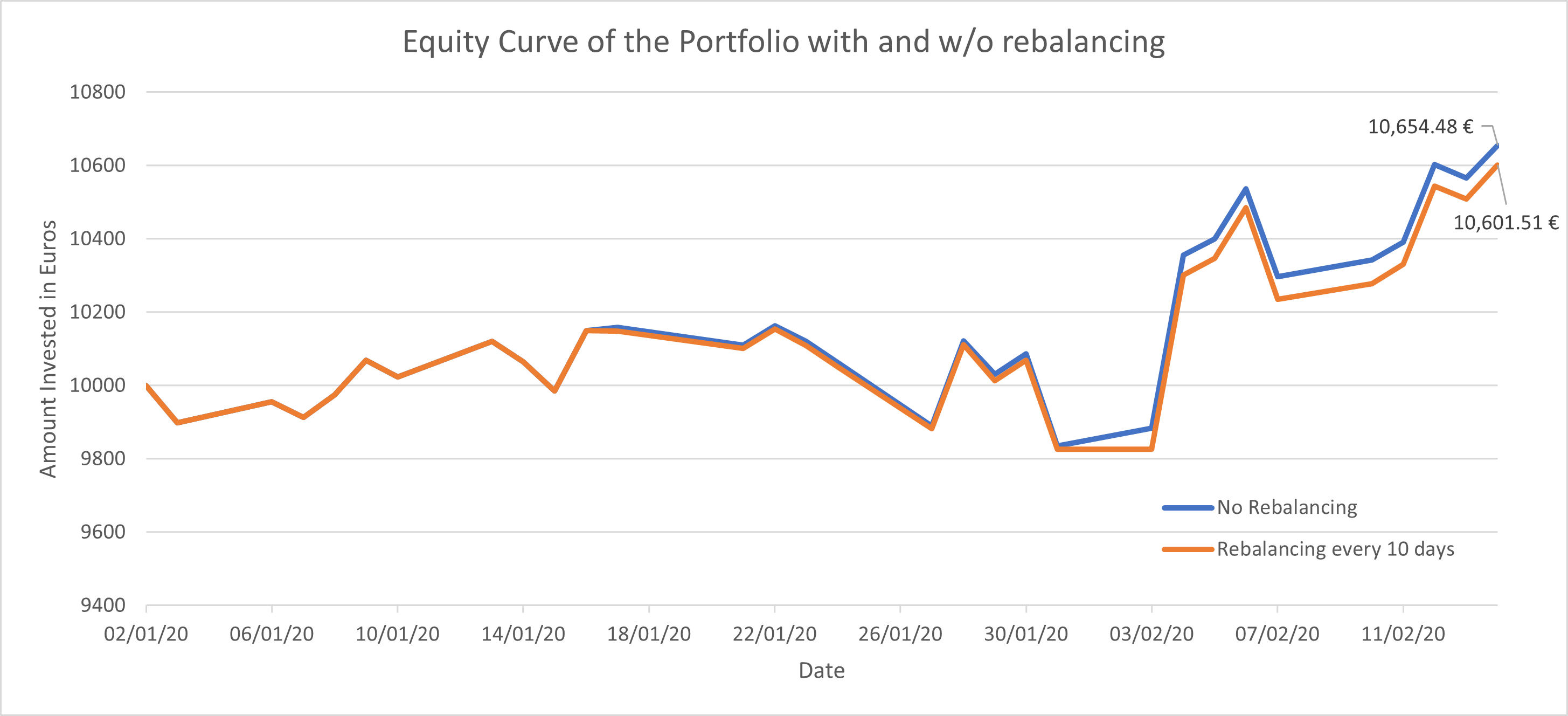
It can be observed that the portfolio returns with rebalancing has reduced. However, it’s imperative to understand that sustaining the risk profile proves advantageous in the long run.
Rebalance Signal
The choice of how often and under what conditions to rebalance a portfolio is a critical decision influenced by an investor’s strategy and preferences. Various signals can prompt the need for rebalancing. As illustrated in the example above, one common approach is time-based rebalancing, which can occur on a daily, weekly, monthly, quarterly, or yearly basis.
Another strategy involves rebalancing triggered by deviations in asset weights beyond predefined thresholds. For instance, if an investor sets a threshold of 5%, they would initiate rebalancing when the actual allocation of a specific asset exceeds or falls below this predetermined threshold.
A third method involves adjusting positions based on the percentage of a specific asset relative to the total portfolio value. For example, if an investor determines that a particular asset should not surpass 10% of the portfolio’s total value, they would rebalance the portfolio whenever the asset’s percentage exceeds or falls below this predefined level.
These are just a few examples, and there could be additional, more specific rebalancing signals triggered by specific events.
Backtesting and Rebalancing
A backtest is a historical simulation of how a strategy would have performed should it have been run over a past period of time. The incorporation of rebalancing in the process of backtesting is essential for creating a realistic simulation of a portfolio’s performance. While backtesting and rebalancing are distinct steps, integrating rebalancing into the backtest simulation is crucial for avoiding bias and obtaining a more accurate reflection of real-world scenarios.
Various rebalancing strategies can be explored and tested during backtesting to assess their impact on portfolio performance. This process aids investors in identifying the optimal rebalancing frequency and making informed decisions about the assets to buy or sell to achieve their investment goals.
Conclusions
Investors must carefully weigh the benefits of rebalancing against these transaction costs, ensuring a net positive impact on the portfolio’s performance. In a dynamic market environment, success lies not only in constructing a robust initial portfolio but also in the ongoing process of rebalancing to navigate the ever-changing financial landscape.
